投資銀行の本格的DCF～エクセル付きで企業価値評価を解説17

DCF法の現在価値計算ステップ4/5です。今回は、将来価値を現在価値に変換し、企業価値を計算します。企業価値の計算には、エグジット・マルチプル（exit multiple）法と永久成長率法の2つがあるので、これら2つの計算方法を解説します。

ステップ4：FCFとターミナル・バリューを現在価値に変換し、企業価値（EV、Enterprise Value）を計算する

最初にFCFの現在価値を算出する

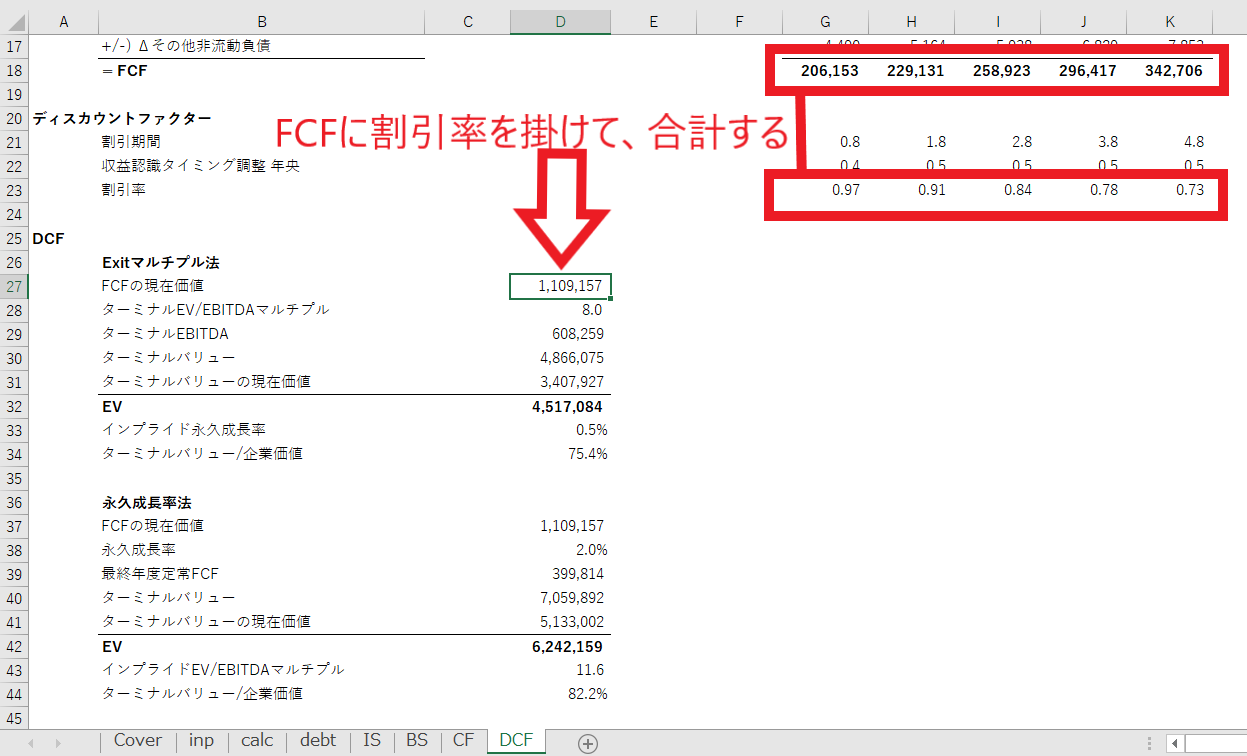
ステップ1で計算したFCFに対して、ステップ3で計算した割引率を乗じて、FCFの現在価値合計を計算します。この計算はエグジット・マルチプル（exit multiple）法と永久成長率法に共通です。

ターミナル・バリューとは、業績予想期間以降の企業価値のこと

企業価値は、その企業が将来生み出す価値の合計を現在価値にしたものです。当初の5～10年間については、オペレーティングモデルでキャッシュフローを予想しますので、その値を現在価値にすればよいのですが、企業はそれ以降も存続して価値を生み出し続けますので、その期間の価値は別途計算する必要があります。この、予想期間以降の価値のことをターミナル・バリューといいます。

冒頭で書きましたが、このターミナル・バリューの計算には、エグジット・マルチプル（exit multiple）法と永久成長率法の2つがあります。投資銀行では、どちらか一方ではなく両方を計算することが多いです。

エグジット・マルチプル法によるターミナル・バリューの計算方法

エグジット・マルチプル法とは、予想期間最終年度の利益に対して、その時点で企業を売却した際に予想される利益マルチプルを掛けて、ターミナル・バリューとする方法です。M&Aの世界ではEV / EBITDAマルチプルが一般的ですが、業種やその他の事情でPERなど別のマルチプルを使うこともあります。

使用するマルチプルは、過半数の株式を取得するマジョリティディールの場合は、過去の類似取引の平均値や中央値を使いますが、過半数未満のマイノリティディールの場合は、類似企業の平均値や中央値、またはその企業自身のマルチプルを使用します。

なぜこのような使い分けをするかというと、マジョリティディールには、企業の支配権を獲得するにあたってのコントロールプレミアムがつくため、マルチプルが上昇する傾向にあるためです。一方で、類似企業の現在の値は、その企業の株を1単位取引する場合のマルチプルなので、マイノリティディールに使われます。

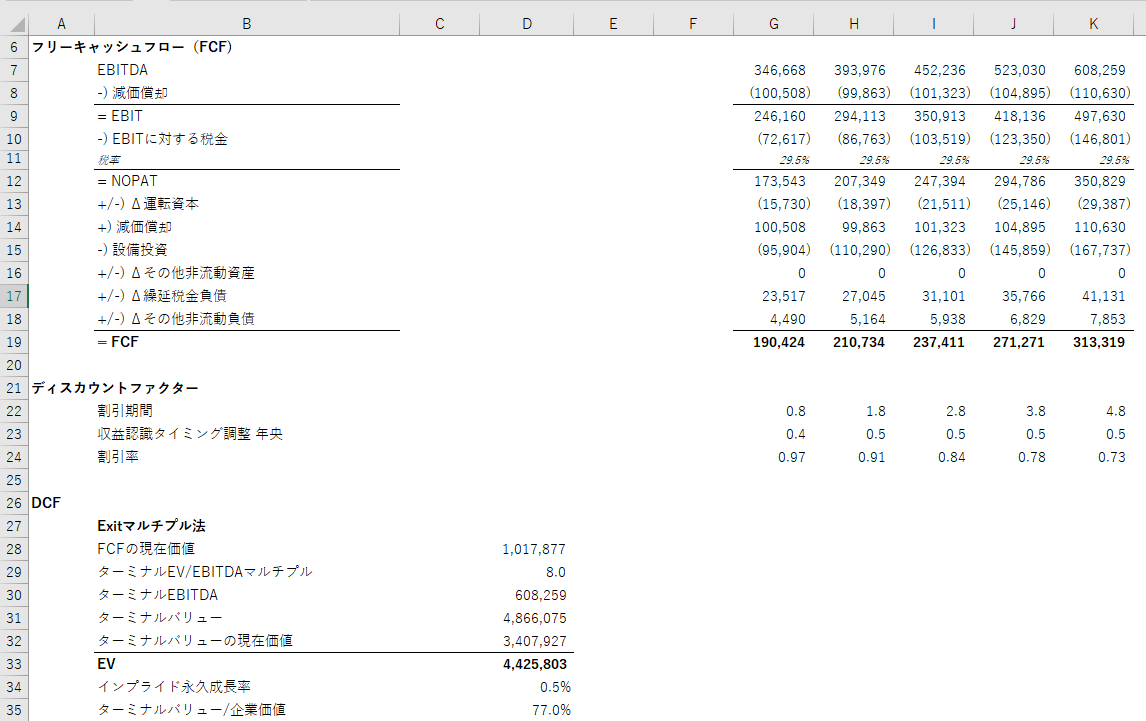
EV / EBITDAマルチプルを例にとると、予想最終年度のEBITDAに対して、予想されるEV / EBITDAマルチプルを乗じて予想最終年度末時点の企業価値（EV）を計算します。このEVを現在価値に割り引くのですが、ここで1つ注意しなければならないことがあります。このEVは予想最終年度末時点の価値なので、前のステップで計算した年央調整後の割引率ではなく、調整前の割引率を使用しなければなりません。

私のモデルのDCFシートD31セルを見ていただくと、K23セルで計算した割引率ではなく、このセルの中で別に割引率を計算しているのがわかると思います。

このようにして計算したターミナル・バリューとFCFの現在価値を合計したものが、エグジット・マルチプル法による企業価値になります。

なお、33行目で計算しているインプライド永久成長率というのは、エグジット・マルチプル法で計算された企業価値が、永久成長率法の場合には何％の永久成長率と同等の水準かを算出したものになります。この数字が小さすぎたり大きすぎたりする場合は、マルチプルの設定が適正ではない可能性があります。

永久成長率法によるターミナル・バリューの計算方法

永久成長率法は、業績予想最終年度以降は、一定の成長率で永久に成長し続けることを前提とした計算方法になります。

まずは、予想最終年度のFCFを用いて、定常状態のFCFを計算します。定常状態とは、一定の成長率で安定的に成長し続ける際のFCFです。具体的な計算方法としては、設備投資と減価償却の値が釣り合って安定している状態を想定し、最終年度のFCFから設備投資と減価償却を控除した値を使用しますが、単純に最終年度のFCFをそのまま使用しているケースも見かけます。

最終年度におけるターミナル・バリューは、以下の計算式で算出します。

～永久成長率法によるターミナル・バリューの計算式～

TV = FCF_最終年度 × (1 + 永久成長率) / (WACC – 永久成長率)

永久成長率は2～4％程度で設定することが多いです。一番低く見積もるのであれば、その国の長期インフレ率を使用するとよいと思いますが、企業はインフレ率以上の成長を目指して努力するので、インフレ率＋αで置いてもよいと思います。

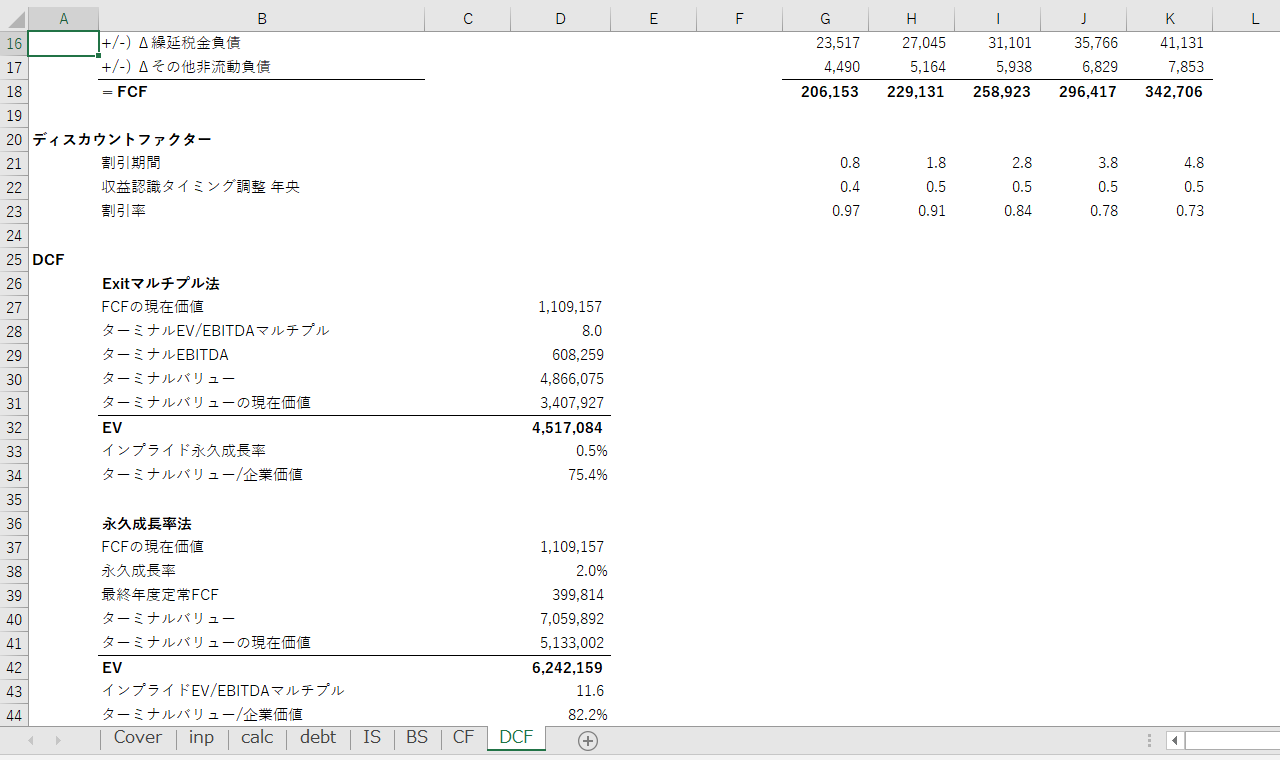
永久成長率のターミナル・バリューは、ステップ3で計算した、年央調整後の最終年度の割引率をそのまま使用できます。

43行目では、エグジット・マルチプル法とは逆に、永久成長率法による企業価値から逆算されるEV / EBITDAマルチプルを計算しています。

これで企業価値（EV、Enterprise Value）が計算できました。

次のステップ

前のステップ

エクセルをダウンロードしてない方は、ダウンロードページからダウンロードしてください。