DCF法の現在価値計算ステップ2/5です。
前回計算したFCFを現在価値に割り引くための割引率であるWACCの計算方法を解説します。
DCFの5つのステップ
- アンレバード・フリー・キャッシュフロー(FCF)を計算する
- WACCを計算する
- WACCを元に各年の割引率を計算する
- FCFとターミナル・バリューを現在価値に変換し、企業価値(EV、Enterprise Value)を計算する
- EVから株式価値を計算する
WACCを計算する
WACCの計算式は1つずつ分解するとわかりやすい
WACCの計算式は、以下のとおり文字ばかりで長たらしいので、慣れない人にはわかりにくいと思いますが、1つずつ意味を分解すると理解しやすくなります。
WACCの計算式
WACC = [Ke × E / (D + E)] + [Kd × (1 – T) × D / (D + E)]
- Ke:株主資本コスト
- E:株式(時価)
- D:負債(時価)
- Kd:負債資本コスト
- T:税率
では、WACCの計算式を分解してみてみましょう。
Ke(株主資本コスト)は株主が会社に要求するリターン
Ke(株主資本コスト)は、株主が会社に対して要求するリターンを指します。
しかし、実際に全ての株主にインタビューして「あなたがこの会社に期待するリターンは何%ですか?」と聞くことは現実的ではありません。
なので、CAPM(Capital Asset Pricing Model)という理論を使って推計します。
CAPMによるKeの計算
Ke = Rf + [βlev × (Rm – Rf)]
- Rf:リスクフリーレート
- βlev:レバードベータ
- Rm:マーケットリスクプレミアム
Rf(リスクフリーレート)は、無リスク資産の代表である長期国債の利回りを使います。
どの国の企業を評価するかによりますが、流動性の高さから10年国債が使われることが多いと思いますが、20年や30年国債を使うケースもあります。
米国のように10年以上の超長期国債の流動性が高い場合は20年債を使うこともあります。
また日本のようにマイナス金利で10年国債が日銀のコントロール下に置かれている場合、10年国債金利が正常な状態の金利水準を反映していないので、やはり20年や30年の超長期国債を使うことになります。
βlev(レバードベータ)は、企業の株価が市場の株価全体(TOPIX等)と比較してどのくらいのボラティリティがあるかという値です。
企業が上場している場合は、その企業のβlevをエクセルで自分で計算することもできますし、ブルームバーグ等を使用できる方は容易に値を入手できます。
ただし、過去の株価を用いて計算したβは、過去一定期間の株価(=サンプル)を用いて統計的に計算したものであるため、推定誤差が生じます。
このため、上場企業であっても、以下で説明する未上場企業のβ算出方法を用いる方が統計的に誤差が少なくなると考えられます。
未企業のβを算出する場合は、事業内容が類似している複数の上場企業のβを計算して、そこから対象企業のベータを推計することになります。
ただし、ベータは負債の多寡で変動する(負債が大きいほどレバレッジが高くなり、ベータが高くなる)ので、類似企業のベータは対象企業にはそのままは使えません。
そこで、類似企業のベータを、一旦無借金状態のベータ(βu、アンレバード・ベータ)に戻して(アンレバリング)から、対象企業の負債比率に応じたベータ(βlev)に戻す(リレバリング)という計算が必要になります。
ベータのアンレバリングとリレバリングの計算式
アンレバリング:βU = βlev / [1 + D / E × (1 – T)]
リレバリング:βlev = βu × [1 + D / E × (1 – T)]
なお、修正βという考え方があり、ベータは最終的には市場平均である1に収斂するという考え方に基づき、算出したβlev(未修正β)に2/3を乗じてから1/3を足すという計算をする場合があります。
どちらのベータを使用するかは各企業の判断による部分もあるかもしれませんが、投資銀行では修正βを使用することが多いと思います。
修正βの計算式
修正β = 未修正β × 2 /3 + 1 / 3
Rm(株式期待収益率)は、株式に対して投資家がどれだけのリターンを期待しているかという数字です。
Rm – Rfとなると、投資家が無リスク資産に対してどれだけの超過リターンを株式に求めるかという数字となります。
この値を直接観測することは難しいので、一般的にはIbbotsonという調査会社のデータ(有料)や、ニューヨーク大学のDamodaran教授のデータ(無料)を使うことが多いです。
E / (D + E)は総資産に占める株式の比率
この値は、上場会社であれば直近決算期の値を使うか、中期的に負債比率が変動することが見込まれる場合は、変動後の将来目標値を使います。
一方で、未上場企業の場合、特に中小企業の場合は、負債比率が最適化されていない可能性があるので、βを算出する際に使用した類似企業の平均や中央値の比率を使うことになります。
Kd × (1 – T)はタックスシールド考慮後の負債コスト
Kd(負債コスト)は、実際の借入金利を用いればいいのですが、WACCの計算ではタックスシールドを考慮する必要があります。
タックスシールドとは、支払利息が利益を減少させることで生じる減税効果のことを指します。
つまり、借入金利はX%だとしても、その金利支払いはその分利益を減少させるので税金が安く済むため、実質的な金利負担はX% × (1 – T)になるというものです。
D / (D + E)は総資産に占める負債の割合
これはE / (D + E)と表裏一体なので、詳細な説明は割愛します。
WACCのエクセルでの計算方法
最後に、エクセルでどのように計算しているかを見ていきましょう。
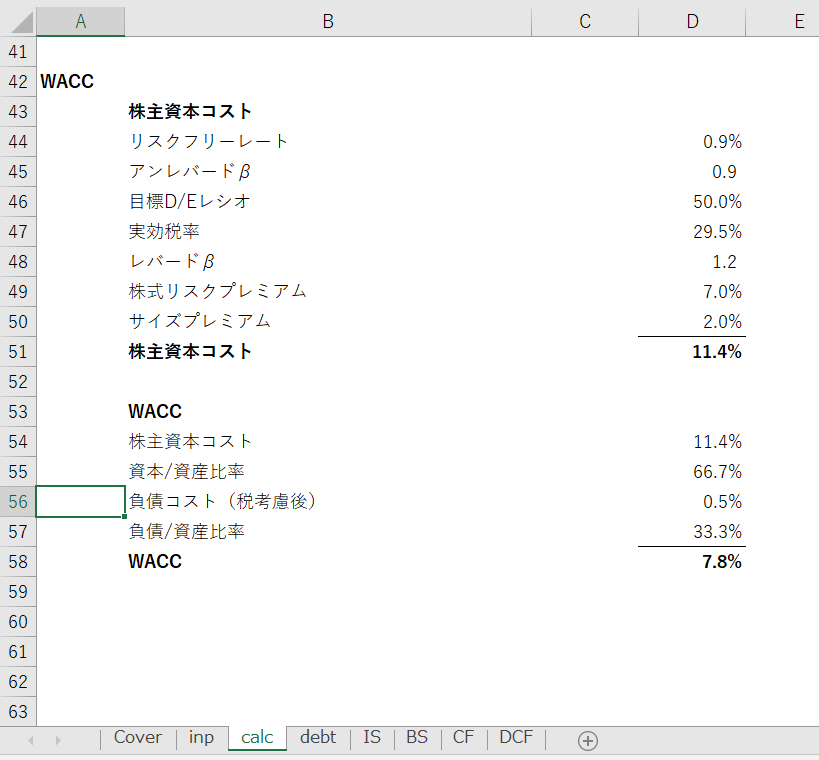
私のモデルでは、calcシートでWACCを計算しています。
アンレバードβは数字を手打ちしていますが、実際の算出方法は先ほど説明したとおりです。
投資銀行で使われるテクニック的なものですが、WACCを含めDCFは多くの前提を用いて計算するので、最終的なアウトプットは1つの値ではなくレンジで示すようにしています。
WACCであれば、7%~9%で0.5%刻みで変化した場合の企業価値をそれぞれ示した表を作成したり、フットボールチャートと呼ばれる最高と最低の値を帯状に示したグラフを用いたりします。
以上、今回は数式が多く、少し複雑だったかもしれませんが、繰り返し読んでいただければ少しずつ理解が深まると思います。
エクセルをダウンロードしてない方は、ダウンロードページからダウンロードしてください。

